Конспект урока по теме "Зависимости между тригонометрическими функциями одного и того же аргумента"
Предмет: Алгебра и начала математического анализа
Учебник: Муравин Г.К., Муравина О.В. Алгебра и начала математического анализа. Базовый уровень.
Тема: Зависимости между тригонометрическими функциями одного и того же аргумента
Тип урока: изучение нового материала
Предметные цели: сформировать представления о тригонометрических тождествах; способствовать совершенствованию вычислительных навыков, навыков подстановки и замены; научить применять тригонометрические тождества для решения задач; сформировать умения вычислять значения тригонометрических функций по известному значению одной из них; научить выражать одну тригонометрическую функцию через другую.
Личностные цели: способствовать развитию умения анализировать, сравнивать знания и умения обучающихся о тригонометрических тождествах; развивать способности к содержательному обобщению и рефлексии; развивать внимательность, трудолюбие и упорство в достижении поставленных целей.
Метапредметные цели: способствовать умение самостоятельно определять цели своего обучения, ставить и формулировать для себя новые задачи в учебе и познавательной деятельности; развивать мотивы и интересы познавательной деятельности; развивать умение соотносить свои действия с планируемыми результатами, осуществлять контроль своей деятельности в процессе достижения результата.
Этап урока | Деятельность учителя | Деятельность ученика | Записи в тетрадях | Записи на доске |
Организационный этап | Здравствуйте. Пожалуйста, проверьте свою готовность к уроку. Присаживайтесь. Откройте рабочую тетрадь и запишите число, «классная работа» | Проверяют готовность к уроку. Присаживаются. Делают записи в тетрадях. | 17.02.2020 | 17.02.2020 |
Этап актуализации темы | Какие тригонометрические функции вы знаете? Скажите, какому отношению равен тангенс угла? А котангенс? Да, действительно. Не трудно заметить, что между тригонометрическими функциями существуют определенные зависимости. Отсюда и вытекает сегодняшняя тема урока. | Синус, косинус, тангенс, котангенс. Синус деленый на косинус. Косинус на синус. | | |
Основной этап | Запишем ее в тетрадь: «Зависимости между тригонометрическими функциями одного и того же аргумента». Запишите, что Не трудно заметить, что эти равенства выражают соотношения между тригонометрическими функциями одного и того же аргумента Если дано значение синуса и косинуса сможем найти тангенс и котангенс? Каким образом? Да. Именно так. Перемножьте равенства, которые мы записали. Чему равно произведение тангенса на котангенс? Верно. Тангенс и котангенс одного и того же угла связаны между собой равенством: Запишите его в тетрадь. Выделите полученную зависимость зеленой ручкой. Это не единственная зависимость между тригонометрическими функциями. Рассмотрим следующие зависимости. Что это за уравнение Верно. Запишите в тетрадь это уравнение. Что связывает между собой данное уравнение? Из курса геометрии 9 класса вспомним, чем является синус? Косинус? То есть Подставьте эти значения в уравнение единичной окружности. Что получилось? Действительно. Получилась еще одна зависимость, которую мы вывели. Эта зависимость называется основным тригонометрическим тождеством. Запишите его, выделите зеленой ручкой и подпишите ее название. Из основного тригонометрического тождества очевидным образом получают следующие тождества:
Каким образом это получили? Запишите тождества в тетрадь и выделите. Запишем вновь основное тригонометрическое тождество: Поделите почлено его на Что вы получили? Именно. Получили еще одно тождество. Выделите его. А если основное тригонометрическое тождество поделить на Данное тождество выделите аналогично. Мы с вами рассмотрели ряд тождеств, связывающие между собой тригонометрические функции. Как вы заметили, они все выводятся из основного тригонометрического тождества. Попрошу вас дома выписать все эти тождества на плотную бумагу (картон) и вложить в тетрадь. Так будет удобнее ими пользоваться и не придется листать учебник. | Записывают тему. Записывают:
Да. Подставить данные значения в равенства Перемножают. 1. Записывают: Выделяют. Уравнение единичной окружности с центром в начале координат. Записывают Оно связывает абсциссу и ординату любой точки данной окружности. Ординатой. Абсциссой. Записывают: Подставляют. Говорят: Записывают, обводят, подписывают: С помощью переноса слагаемого в правую часть, со сменой знака. Записывают Записывают. Делят. Говорят: Выделяют. Вычисляют. Говорят: | Зависимости между тригонометрическими функциями одного и того же аргумента.
| Зависимости между тригонометрическими функциями одного и того же аргумента.
|
Этап закрепления темы | Рассмотрим примеры, которые иллюстрируют применение данных тождеств. №1. Найдите (учитель решает у доски) Для нахождения Именно, подставляем то, что дано по условию. А что дано? Подставляем. Условие Косинус второй четверти какой знак имеет? А значит Записываем Найдем
Ответ: Самостоятельно решите следующий пример. №2. Найдите Сверьте ответы с ответами на доске. (учитель просит объяснить решение) У кого не получилось? (если у нескольких человек не получилось, выноситься решение на доску). Следующий пример, который наглядно иллюстрирует применение данных тождеств. Записываем. №3. Докажите тождество: Записываем: «доказательство:» Преобразуем левую часть равенства.
Заменяем,
Получаем, Доказали. Итак, откройте теперь учебник на странице 169, решаем номер 354, пункты 1,2,5,6,9,10. (учащиеся решают у доски, учитель при необходимости помогает) Есть ли вопросы по данному номеру? Следующий номер 356, пункты 1и 2. (учащиеся решают у доски, учитель при необходимости помогает). Хорошая работа. Вы молодцы. | Записывают условие задачи.
Минус
Записывают ход решения задачи. Решают. Ответ учащихся. Записывают условие. Записывают ход решения.
Решают. №354. 1) 2) 5) 6) 9) 10) Ответ учащихся. Решают. №356. 1) Чтобы доказать тождество нужно доказать, что разность левой и правой части равна нулю.
2) Преобразуем правую часть.
Правая часть равна левой. Доказали. | №1. Найдите Решение.
Ответ: №2. Найдите Решение.
Ответ: №3. Докажите тождество: Доказательство:
Доказали. №354. 1) 2) 5) 6) 9) 10) №356. 1)
2)
Доказано. | №1. Найдите Решение.
Ответ: №2. Найдите Ответ: №3. Докажите тождество: Доказательство:
Доказали. В классе: №354 (1,2,5,6,9,10) №354. 1) 2) 5) 6) 9) 10) №356. 1)
2)
Доказано. |
Рефлексия | Что вы узнали нового? Сколько тождеств мы выписали? Как вы думаете для чего нужны эти тождества? Действительно, зависимости между тригонометрическими функциями позволяют по значению одной из функции находить значения остальных тригонометрических функций при том же значения аргумента. Запишите домашнее задание. №354 (3,4,7,8,11,12),№356(5-8). Посмотрите на домашнее задание. Есть ли вопросы по нему? Спасибо за урок. До свидания. | Ответ учащихся. 6 Ответ учащихся. Ответ учащихся. | Д/з №354 (3,4,8,9,12,13) №356(5-8) | Д/з №354 (3,4,8,9,12,13) №356(5-8). |


 и
и  .
. .
.  .
. ?
?  ;
;  .
.
 .
. .
. .
. , что получим?
, что получим? .
.


 ;
; 
 ,
, ,
, 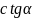 , если известно, что
, если известно, что  и
и  .
. . Чему отсюда равен
. Чему отсюда равен  может являться углом второй, третий или четвертой четверти. Однако
может являться углом второй, третий или четвертой четверти. Однако  в данной задаче положителен, а значит, –угол второй четверти.
в данной задаче положителен, а значит, –угол второй четверти. .
. .
. .
. ;
;  ;
;  .
. и
и 

 что это?
что это? )
) это?
это? )=
)= .
. .
. .
. .
. .
.




 .
. .
. . Доказано.
. Доказано.
 .
. .
. .
. . (так как
. (так как  .
. .
. .
. ;
;  .
. =
=