"Квадратное уравнение. Решение уравнений, сводящихся к квадратным"

1. ИНФОРМАЦИЯ О РАЗРАБОТЧИКЕ ПЛАНА

2. ОБЩАЯ ИНФОРМАЦИЯ ПО УРОКУ

3. БЛОЧНО-МОДУЛЬНОЕ ОПИСАНИЕ УРОКА

Этап 1. Организационный этап

Здравствуйте, ребята! Сегодня на уроке мне хотелось бы вас пригласить более глубже заглянуть в замечательный мир математики – в мир уравнений, в мир поиска, в мир исследований.

Этап 2. Актуализация знаний

Именно сегодня надо взять свои знания и применить их на практике, потому что на нашем уроке мы обобщим все знания и покажем все наши умения по теме. Как говорил А. Эйнштейн «Мне приходится делить время между политикой и уравнениями. Однако уравнения, по-моему, гораздо важнее. Политика существует только для данного момента, а уравнения будут существовать вечно». И решать их нужно правильно. Как вы уже поняли, какая у нас тема урока? Что нам с вами предстоит сегодня сделать? (примерный ответ: мы повторим теоретический материал по данной теме, повторим и обобщим способы решения квадратных уравнений (как полных, так и неполных, решение рациональных уравнений, кубических и биквадратных уравнений) (Слайд 1) (Приложение 1)

Чтобы выполнить всё намеченное, вы должны быть активны и бодры, и для этого мы сейчас проведём такие упражнения:

1. Сложите ладони, интенсивно потрите их (это упражнение способствует мобилизации энергетического потенциала и работы всех внутренних органов, т.к. на ладонях находится много биологически активных зон).

2. Раздвиньте указательный и средний пальцы на обеих руках, просуньте между ними уши и с силой растирайте кожу, этот массаж улучшит ваше зрение и активизирует работу головного мозга. Теперь вы готовы к активной и плодотворной работе. Сначала давайте проверим ваши теоретические знания по данной теме. Внимание! (Слайд 2)

Блиц-опрос! Ответьте правильно на вопросы и будьте победителями в самых разных номинациях! Но за правильно данный ответ вы не только получите звание, но еще и фишку. Фишки нам нужны, ребята, для того, чтобы в конце урока мы с вами могли правильно друг друга оценить и получить отметки.

Вопросы:

1. Какое уравнение называется квадратным? (примерный ответ: квадратным уравнением называют уравнение вида ах2 + bх + с = 0, где коэффициенты а, b, с – любые действительные числа, причём а ≠ 0. Коэффициенты различают по названиям: а – первый или старший коэффициент, b – второй коэффициент, с – свободный член. За правильный ответ учащийся становится победителем в номинации «Ума палата», за неправильный – «Невыносимая легкость бытия»).

2. Какое квадратное уравнение называется приведённым, а какое – неприведённым? (примерный ответ: квадратное уравнение называется приведённым, если его старший коэффициент равен 1, неприведённым – если первый коэффициент отличен от 1. За правильный ответ учащийся становится победителем в номинации «Он наш супермен», за неправильный – «Я вам пишу, чего же боле»).

3. Какие ещё квадратные уравнения, кроме приведённых и неприведённых, различают? (примерный ответ: Полные и неполные квадратные уравнения. За правильный ответ учащийся становится победителем в номинации «Наш человек», за неправильный – «В начале славных дел»).

4. Какое уравнение является полным? (примерный ответ: полное квадратное уравнение – это квадратное уравнение, в котором присутствуют все 3 слагаемых или в котором второй коэффициент и свободный член не равны 0. За правильный ответ учащийся становится победителем в номинации «Пытливый ум», за неправильный – «Наш пострел везде поспел»).

5. Какое уравнение называется рациональным? (примерный ответ: рациональное уравнение – это уравнение, в левой части которого стоит рациональное выражение, составленное из чисел и переменной х с помощью операций сложения, вычитания, умножения, деления, возведения в степень, а в правой части стоит 0. За правильный ответ учащийся становится победителем в номинации «Скрытые резервы», за неправильный – «Крепкий орешек») (Слайды 3-7).

Этап 3. Мотивация учебной деятельности учащихся

Молодцы! Мы вот с вами повторили сейчас теорию, но кое-что забыли обсудить. Где еще нам нужны уравнения, кроме уроков алгебры? Правильно, и на геометрии, чтобы с их помощью найти, например, стороны прямоугольного треугольника, и на физике, чтобы рассчитать время полета мяча до определенной высоты, и даже на ЕГЭ по химии квадратные уравнения помогут решить вам задачи. Как это может быть неинтересно?

Этап 4. Первичное закрепление

А теперь предлагаю вспомнить способы решения уравнений на практике. К доске будут выходить ребята, которые не были задействованы в опросе, а остальные решают в тетради. За каждое верно решенное уравнение вы можете так же получить фишки. (Слайд 8).

Примеры:

1. x2 – 1 = 0

2. x2 – 10x + 9 = 0

3. 18y3 – 36y2 = 0

4. (x2 – 10)2 – (x2 – 10) – 4 = 0

Этап 5. Творческое применение и добывание знаний в новой ситуации

Прекрасно! Продолжаем. (Слайд 9) Михаил Васильевич Ломоносов говорил: «Теория без практики мертва и бесплодна. Практика без теории невозможна и пагубна. Для теории нужны задания, для практики сверх того, и умения». И теперь вы должны, проявить свои знания при решении квадратных уравнений и умение работать в команде. Сейчас я предлагаю вам объединиться в команды: 1 парта со 2 партой, 3 с 4 и т.д. (всего 5 команд). (Слайд 10)

На доске вы видите некоторую недостроенную фигуру, которую нам предстоит восстановить! Каждой группе я раздаю карточки, где написаны 4 уравнения. Применив все свои знания и силы, помогая друг другу в затруднительных ситуациях и выполняя взаимопроверку, вы сможете справиться с этой задачей. И так, посмотрите, пожалуйста, на ваши карточки (Приложение 2). Решив уравнения, каждый из вас получит их корни, которые необходимо поставить в пару к нужной букве. Далее вы по очереди выходите к доске и закрашиваете вашу комбинацию. Всем удачи!

Правильно! У нас получился самолет! Как же связан самолет с нашей темой? (Примерный ответ: траектория, по которой взлетает самолет, задается квадратным уравнением). Взлет самолета главная составляющая полета. Здесь берется расчет для маленького сопротивления и ускорения взлета. Изучая тему квадратных уравнений, мы как-то не задумывались о том, что квадратные уравнения имеют широкое практическое применение.

Давайте с вами поразмыслим, где же теперь нашли применение квадратные уравнения, если не брать во внимание их изучение в школах и различных ВУЗах. (Выслушиваются варианты учащихся, затем открываются слайды 12,13 и 14).

Этап 6. Диагностика и самодиагностика

Хорошо! Давайте подведем итоги нашего урока, узнаем кто был самый активный и погрузился в мир уравнений, а кто еще только стоит на пороге и боится приоткрыть дверь в этот мир (Подсчитываются набранные фишки и озвучиваются отметки).

Этап 7. Информация о домашнем задании, инструктаж по его выполнению

Квадратные уравнения остаются одним из важнейших инструментов в математике и науке. Их решения способствуют развитию технологий и помогают понимать сложные системы. А будущее внедрение квантовых вычислений и искусственного интеллекта обещает еще более эффективные методы решения и анализа квадратных уравнений. Дома предлагаю вам побольше узнать где и как применяются наши великолепные уравнения.

Этап 8. Рефлексия

«Я»: Как работа? Допускал ли ошибки _______________________«Мы»: насколько мне помогали одноклассники, учитель, а я – им?» _________________________ «Дело»: понял ли материал? Узнал ли больше?_____________________

Я ставлю себе за урок отметку______________________ Я ставлю отметку учителю_____________________________ Мне понравилось на уроке___________________________ Мне не понравилось на уроке____________________________

В заключение мне хотелось бы вам пожелать, чтобы каждый из вас полюбил алгебру так же, как и я, в том числе, чтобы эта тема стала вашим золотым ключиком, с помощью которого перед вами открывались бы любые двери.

Урок окончен. Спасибо за работу. Будьте здоровы!

Приложение 1

Слайд 1

Слайд 2

Слайд 3

Слайд 8

Слайд 10

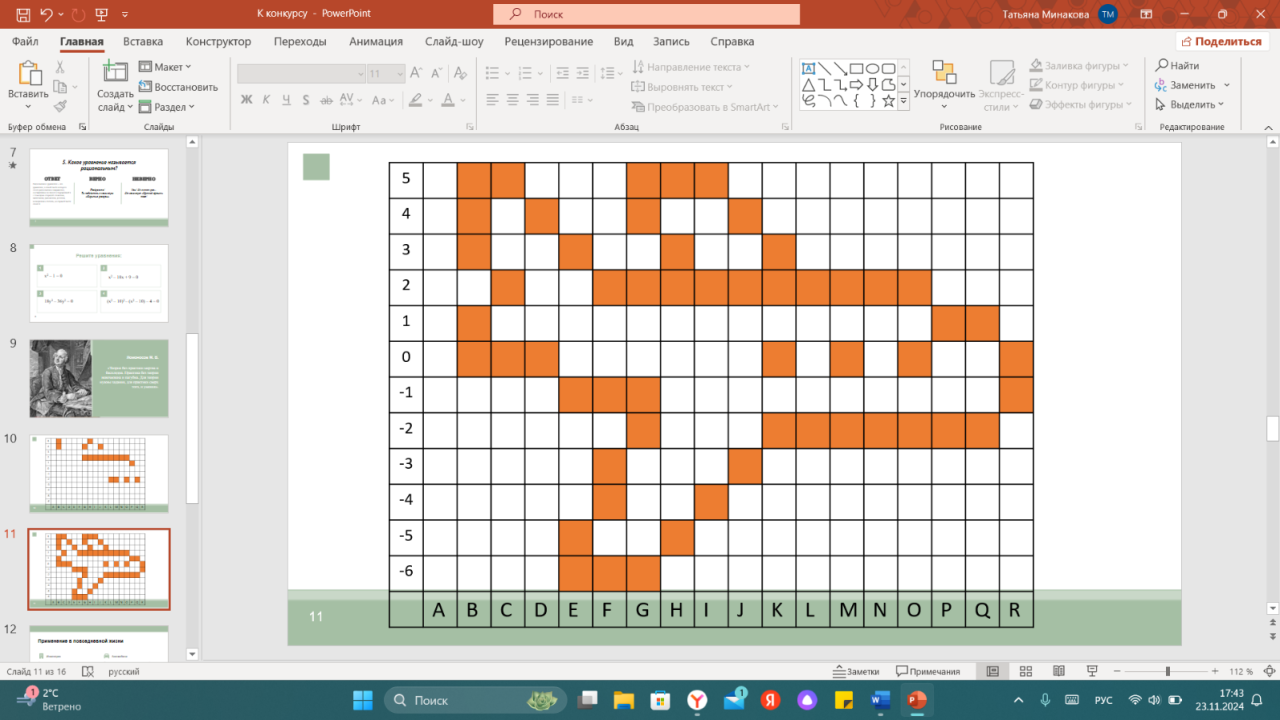
Слайд 11

Слайд 12

Приложение 2