Методическая разработка урока математики по теме «Первообразная»

Государственное бюджетное профессиональное образовательное учреждение
«Кузнецкий многопрофильный колледж»
МЕТОДИЧЕСКАЯ РАЗРАБОТКА УРОКА
ДИСЦИПЛИНА: МАТЕМАТИКА
ТЕМА «Первообразная»
Преподаватель:Мустакаева Г.Р.
Аннотация
Методическая разработка по дисциплине «Математика» по теме «Первообразная» предназначена для реализации государственных требований к минимуму содержания и уровню подготовки студентов по данной дисциплине, которая относится к общеобразовательному циклу.
Методической целью урока является использование инновационных форм и методов на занятиях, анализ дидактической эффективности использования ТС обучения, обобщение приемов научной организации и контроля учебного процесса. Повышение мотивации к обучению с помощью методической редукции, основанной на схемо-знаковой визуализации учебного материала с использованием ИКТ. Повышать интерес к предмету, упрощение восприятие объемного материала посредством использования схем и таблиц. Также для эффективности образовательного процесса используются опорные конспекты, дискуссия, презентация, видеофрагменты.
Содержание
- Структура урока
- Технологическая карта урока
- Результаты апробации
- Литература
Структура урока
- Организационный момент
- Постановка учебной проблемы
- Формулирование проблемы, планирование деятельности
- Открытие новых знаний
- Первичная проверка понимания материала
- Закрепление полученных знаний
- Рефлексия учебной деятельности
- Задание на дом
Технологическая карта урока
Предмет | Математика |
Курс | 1 |
Тема урока | Первообразная |
Тип урока | Изучение и закрепление нового материала |
Вид урока | Комбинированный |
Форма обучения | Классно-урочная |
Форма деятельности | Фронтальная и индивидуальная. |
Цель урока | Введение понятия первообразной и обучение нахождению первообразной,как действию,обратному нахождению производной. |
Задачи урока | 1. Образовательные: организовать деятельность учащихся по применению имеющихся знаний по теме «Производная» к понятию первообразной функции,к определению понятия первообразной функции, к установлению связи между производной и первообразной,повторить понятие производной функции, сформировать у студентов первичные знания по нахождению первообразной 2. Развивающие: развитие у учащихся умений анализировать, устанавливать связи, причины и следствия;развитиевнимания,мышления,самостоятельности,позновательного интереса.;формирование приемов обобщения, алгоритмизации. 3. Воспитательные: формирование у студентов ответственного отношения к учению; воспитывать умение слушать и вступать в диалог, участвовать в коллективном обсуждении проблем, интегрироваться в группу сверстников и строить продуктивное взаимодействие, воспитывать ответственность и аккуратность. |
Оборудование | Мультимедийный проектор |
Методическое оснащение | План-конспект, презентация,учебник. |
Основные термины, понятия | Дифференцирование,первообразная,производная,физический смысл производной |
Продолжительность урока | 90 минут |
Планируемый результат | |
Предметные умения: Знать:
уметь:
| Личностные УУД: - независимость и критичность мышления; - воля и настойчивость в достижении цели.
Метапредметные УУД
|
Дидактические задачи этапов урока
Этапы урока | Дидактические задачи |
Организационный (этап мотивации)(2 мин) |
|
Постановка учебной проблемы (15 мин) |
|
Формулирование проблемы, планирование деятельности (15 мин) |
|
Открытие новых знаний (15 мин) |
|
Первичная проверка понимания материала (10 мин) |
|
Закрепление полученных знаний
|
|
Рефлексия учебной деятельности (3 мин) |
|
Задание на дом (1 мин) |
Формируемые умения | Деятельность преподавателя | Деятельность обучающихся | |||||
Организационный этап | |||||||
Метапредметные (УУД): регулятивные: - самостоятельно прогнозировать свою деятельность, умение настраиваться на занятие коммуникативные: - уметь слушать и вступать в диалог. | Приветствие. Мотивация на изучение новой темы. | Приветствуют преподавателя, проверяют свою готовность к уроку (наличие тетрадей, ручек) | |||||
Постановка учебной проблемы.Формулирование проблемы, планирование деятельности | |||||||
Предметные: знать : определение,производной,понятия приращения функции и аргумента,физический и геометрический смыслы производной; производные элементарных и сложных функций определение первообразной первообразная определяется неоднозначно уметь: находить первообразные функции в простейших случаях проверять, является ли функция F(x) первообразной для функции f(х) на данном промежутке уметь применять полученные знания к решению практических задач. Метапредметные (УУД): познавательные: - уметь самостоятельно определять цели в деятельности в ходе применения понятия производной функции к определению понятия первообразной – анализировать, сравнивать, классифицировать и обобщать факты и явления; - искать и выделять необходимую информацию. Регулятивные: – самостоятельно обнаруживать и формулировать проблему в классной и индивидуальной учебной деятельности; коммуникативные: – самостоятельно организовывать учебное взаимодействие в группе (определять общие цели, договариваться друг с другом и т.д.); - уметь слушать и вступать в диалог. | 1. Определение производной функции
2. Физический смысл производной Из курса физики вспомним ,что такое скорость и ускорение и по каким формулам их находим. 3.Есть путь,есть время-можем найти скорость. 4. Задача 1. Материальная точка движется прямолинейно по закону s(t) = t3 +2t2 – 5t. Найти функцию, выражающую закон изменения скорости движения v(t) 5.Решить обратную задачу.Найти путь. Задача 2. Скорость прямолинейно движущейся точки изменяется по закону v(t)=3 t2 +4t – 5. Найти функцию s(t), выражающую зависимость перемещения точки от времени. Какую функцию S(t) надо продифференцировать? (Вспомнить таблицу и формулы производных) | 1. Производной функции в данной точке называется предел отношения приращения функции в этой точке к приращению аргумента, когда приращение аргумента стремится к нулю. 2. Производная функции y = f(x) в точке x0 – это скорость изменения функции f (х) в точке x0 x'(t). = n(t) v(t)=S/(t)-скорость есть производная пути по времени. 3.Быстрота изменения положения тела в пространстве с течением времени ;V=St, где S зависимая переменная переменная, t-независимая переменная. 4. v(t)=S/(t)=3 t2 +4t – 5. 5. v(t)=S/(t)-скорость есть производная пути по времени. Скорость это результат производной пути по времени. S –это первоначальная величина.Так как, v(t)=S/(t)=3t2 +4t – 5- требуется восстановить функцию S(t)-найти такую функцию,производная которой равняется данной функции. s(t) = t3 +2t2 – 5t. | |||||
Открытие новых знаний | |||||||
Знать: производные элементарных и сложных функций определение первообразной первообразная определяется неоднозначно уметь: находить первообразные функции в простейших случаях проверять, является ли функция F(x) первообразной для функции f(х) на данном промежутке уметь применять полученные знания к решению практических задач. Метапредметные (УУД): познавательные: - уметь самостоятельно определять цели в деятельности в ходе применения понятия производной функции к определению понятия первообразной – анализировать, сравнивать, классифицировать и обобщать факты и явления; - искать и выделять необходимую информацию. Регулятивные: – самостоятельно обнаруживать и формулировать проблему в классной и индивидуальной учебной деятельности; коммуникативные: – самостоятельно организовывать учебное взаимодействие в группе (определять общие цели, договариваться друг с другом и т.д.); - уметь слушать и вступать в диалог. | 1.Первоначальная величина- 2.Определение первообразной 3.Как проверить результат? 4. Как можно изменить первообразную функции,чтобы ее производная оставалась постоянной? 5.Сколько первообразных может иметь функция? 6. Основное свойство первообразных: 7. Используя таблицу производных элементарных функций и основное свойство первообразных,заполните таблицу первообразных | 1.первообразная. 2.Функция F(x) называется первообразной для функции f(x) на заданном промежутке Х, если для всех х из этого промежутка F/(x)= f(x) 3. Найти производную s(t) = t3 +2t2 – 5t S/(t)=3t2 +4t – 5 4. Если вспомнить таблицу производных,то производная константы равна нулю.Если к первообразной функции прибавть константу. s(t) = t3 +2t2 – 5t+С, где С любое действительное число. 5.Множество, т.к. (F(x)+C)’=F’(x)=f(x) 6. если F(x) – первообразная функции f(x) на некотором промежутке, то F(x)+C – первообразная функции f(x) на этом промежутке. 7. | |||||
Первичная проверка понимания материала | |||||||
Предметные: Знать: определение первообразной первообразная определяется неоднозначно уметь: находить первообразные функции в простейших случаях проверять, является ли функция F(x) первообразной для функции f(х) на данном промежутке уметь применять полученные знания к решению практических задач. Метапредметные (УУД): познавательные: – анализировать, сравнивать, классифицировать и обобщать факты и явления. регулятивные: – самостоятельно обнаруживать и формулировать проблему в классной и индивидуальной учебной деятельности. коммуникативные: – самостоятельно организовывать учебное взаимодействие в группе (определять общие цели, договариваться друг с другом и т.д.). | 1) Например, функция F(х) = sin x является первообразной функции f (x) = cos x так как (sin x ) ′ = cos x 3)Функция: f(x) = 3х2 Производная функции: Первообразная функции: В данном примере производная от F(x) = х3 + С будет равна (как в определении): Примеры. 1. Выяснить, является ли функция F (x) = х 3 – 3х + 1 первообразной для функции f(x) = 3(х 2 – 1). 2. Найти все первообразные функции f(x) : а) f(x) = х 4 + 3х 2 + 5 б ) f(x) = sin(3x – 2) в) 3. Для функции f(x) = 4 – х 2 найти первообразную, график которой проходит через точку (-3; 10). Решение примеров к таблице:найти первообразные | 2) F(x)=x4 f(x) = 4x3 3)f´(x) = 3 · 2х = 6х где С -любое действительное число F´(x) = (х3 + С)´ = 3х2 + 0 = 3х2 = f(x) (производная от С = 0, т. к. С — число) 1.Решение: F'(x) = (х 3 – 3х + 1)′ = 3х 2 – 3 = 3(х 2 – 1) = f(x), т.е. F'(x) = f(x), следовательно, F(x)является первообразной для функции f(x). 2. а)Решение: Используя таблицу и правила нахождения первообразных, получим:
Ответ: б)Решение:
Ответ: в)Решение:
Ответ: 3.Решение: 1) Найдем все первообразные функции f(x): 2) Найдем число С , такое, чтобы график функции
Следовательно, Ответ: | |||||
Закрепление новых знаний | |||||||
Предметные: Знать: определение первообразной первообразная определяется неоднозначно уметь: находить первообразные функции в простейших случаях проверять, является ли функция F(x) первообразной для функции f(х) на данном промежутке уметь применять полученные знания к решению практических задач. Метапредметные (УУД): познавательные: – анализировать, сравнивать, классифицировать и обобщать факты и явления. регулятивные: – выдвигать версии решения проблемы, осознавать конечный результат, выбирать средства достижения цели из предложенных или их искать самостоятельно; – подбирать к каждой проблеме (задаче) адекватную ей теоретическую модель. коммуникативные: – самостоятельно организовывать учебное взаимодействие в группе (определять общие цели, договариваться друг с другом и т.д.); – отстаивая свою точку зрения, приводить аргументы, подтверждая их фактами; - уметь слушать и вступать в диалог. | Работа в парах. Найти все первообразные функции: 1. Функция f (x) = x5 2.f (x) = 3/x 3. f (x) = ex 4. f (x) = 4·sin x 5.f (x) = (3x - 4)5 6. f (x) = e -3x+5 7. f (x) = sin (6 — 7x) 8. f (x) = cos (6x — 5) №983,984 учебника | 1. 2. F (x) = 3 ln x + C 3. F (x) = ex + C
4. f (x) = 4·sin x 5
6. F (x) = e -3x+5 + C 7. F (x) = ·(- cos (6 - 7x)) + C = cos (6 - 7x) + C 8. F (x) = ·sin (6x — 5) + C | |||||
Рефлексия учебной деятельности | |||||||
Предметные: Знать: определение первообразной первообразная определяется неоднозначно уметь: находить первообразные функции в простейших случаях проверять, является ли функция F(x) первообразной для функции f(х) на данном промежутке уметь применять полученные знания к решению практических задач. Метапредметные (УУД): познавательные: – классифицировать и обобщать факты и явления; – строить логически обоснованное рассуждение, включающее установление причинно-следственных связей. регулятивные: – осознавать конечный результат решения проблемы. коммуникативные: – самостоятельно организовывать учебное взаимодействие в группе (определять общие цели, договариваться друг с другом и т.д.); - уметь слушать и вступать в диалог. | Преподаватель: - Что вы сегодня узнали нового? - Какова была цель вашей деятельности? - Вы достигли поставленной цели? - Что вы использовали, и что вам помогло в достижении цели? -Все, кто отвечал на уроке будут оценены. | Возможные варианты ответов: Производная –«производит» новую функцию. Первообразная - первичный образ.
Определение производной функции,ее физический смысл. | |||||
Задание на дом | |||||||
Урок № 22 https://resh.edu.ru/subject/lesson/3993/start/225744/ | |||||||
3. Результаты апробации работы.
3.1 Оценка актуальности и значимости методической разработки.
В настоящее время постоянно встает вопрос о применении новых технологий в обучении. Данная методическая разработка рассчитана на использование ИКТ, сочетание фронтальной, групповой и индивидуальной форм работы со студентами, использования проблемного обучения. Обозначенные идеи стандарта нового поколения реализуются через
осуществление деятельностного подхода в обучении общеобразовательным дисциплинам.
Данная методическая разработка урока ориентирована на достижение оптимального усвоения знаний по дисциплине
«Математика»
Предметное содержание урока соответствует образовательным и воспитательным целям. Каждый этап урока комбинирует различные формы работы с учебным материалом: индивидуальную, групповую, фронтальную.
Задания направлены на решение следующих развивающих задач:
- развитие личностных качеств студента;
- развитие внимания, мышления, логики, памяти;
- развитие познавательных способностей, овладение умением взаимодействовать группе;
- повышение финансовой грамотности и мотивации к активной познавательной деятельности;
- развитие умений систематизировать полученные знания.
3.2 Ход апробации.
Представленный выше урок был апробирован в ходе освоения дисциплины «Математика» среди учащихся первого курса.
Цели:
1) определить, как повлияет урок на мотивацию студентов к обучению данной дисциплины;
2) узнать, способствуют ли использованные методы и приемы лучшему освоению учебного материала;
3) определить рациональность спланированных уроков с применением компьютера и новых информационных технологий.
Апробация осуществлялась в группах студентов 1-ого курса, обучающимся по специальности «Дошкольное образование» «Физическая культура».
Результаты апробированных уроков позволили сделать следующие выводы:
1) использование ИКТ вызывает у студентов повышенный интерес, способствует повышению активности на уроке и лучшему освоению материала;
3) сочетание индивидуальной, групповой и фронтальной работы позволяет задействовать на уроках всех студентов .
Литература и источники информации
1.Алгебра и начала анализа: учеб. для 10-11 кл. общеобразоват. учреждений/ Ш.А. Алимов, Ю.М. Колягин, Ю.В. Сидоров и др. М.: Просвещение, 2007.
2.https://resh.edu.ru/subject/lesson/3993/start/225744
3. https://www.yaklass.ru/materiali?mode=lsntheme&themeid=1


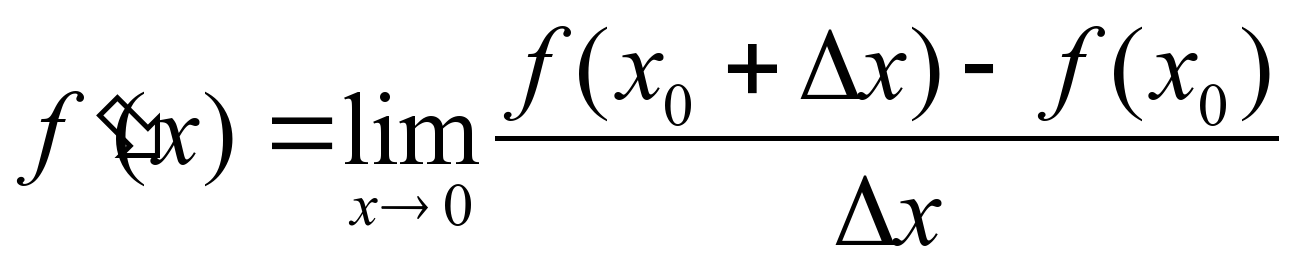








 проходил через точку (-3; 10). Подставим х = – 3, y = 10 , получим:
проходил через точку (-3; 10). Подставим х = – 3, y = 10 , получим:
 .
.